1. Đặt vấn đề
Thuật toán Dijkstra là một trong những thuật toán cổ điển để giải quyết bài toán tìm đường đi ngắn nhất từ một điểm cho trước tới tất cả các điểm còn lại trong đồ thị có trọng số. Trong bài viết này chúng ta cùng tìm hiểu ý tưởng cơ bản của thuật toán Dijkstra.
Mỗi ngày, khi mở Google Maps để tìm đường đến một nơi nào đó, ta thường thấy ứng dụng chỉ trong vài giây đã đề xuất tuyến đường ngắn nhất — đôi khi còn kèm cả thời gian di chuyển dự kiến. Nghe có vẻ đơn giản, nhưng nếu suy nghĩ kỹ, bài toán đằng sau đó không hề nhỏ: giữa hàng trăm con đường, hàng ngàn ngã rẽ, làm thế nào máy tính biết được con đường nào là ngắn nhất?
Đó chính là bài toán đường đi ngắn nhất trong đồ thị có trọng số — một trong những bài toán kinh điển của khoa học máy tính.Và lời giải nổi tiếng nhất cho nó chính là thuật toán Dijkstra, được nhà khoa học người Hà Lan Edsger W. Dijkstra giới thiệu vào năm 1959.
2. Graph
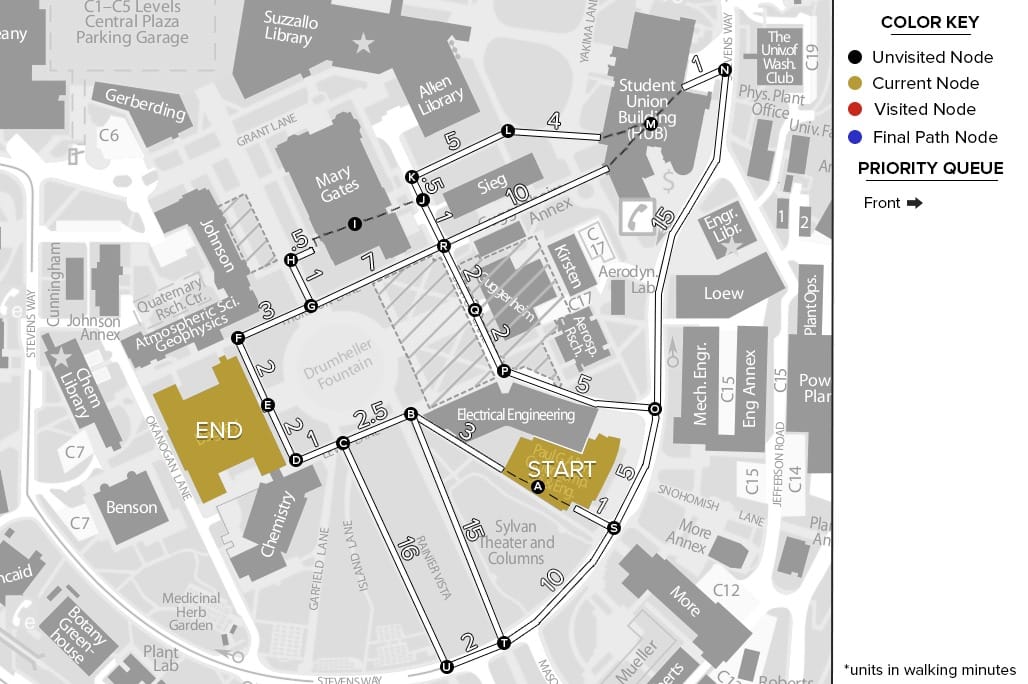
Trước khi đi sâu vào cách hoạt động của Dijkstra, chúng ta cần hiểu nền tảng mà nó dựa vào — lý thuyết đồ thị. Bởi vì bản chất của bài toán tìm đường ngắn nhất không chỉ là phép tính, mà là việc di chuyển giữa các “điểm” được kết nối với nhau bằng các “đường”. Trong ngôn ngữ toán học, tập hợp các điểm và đường nối đó chính là đồ thị. Và thuật toán Dijkstra áp dụng cho các bài toán có trọng số không âm.
Hãy tưởng tượng bạn đang ở Hà Nội và muốn tìm đường đến Đà Nẵng. Trên bản đồ, mỗi thành phố là một điểm, và các tuyến đường là những đoạn nối giữa chúng. Mỗi tuyến có độ dài hoặc thời gian di chuyển khác nhau — chính là “trọng số” của các cạnh trong một đồ thị có trọng số. Đó chính là mô hình mà thuật toán Dijkstra sử dụng để tính toán đường đi ngắn nhất.
3. Ý tưởng thuật toán
Dijkstra hoạt động dựa trên hai nguyên tắc đơn giản:
- Greedy: luôn chọn đỉnh có khoảng cách tạm thời nhỏ nhất tính từ điểm xuất phát.
- Relaxation: nếu tìm thấy một con đường ngắn hơn đến đỉnh kề, thì cập nhật lại khoảng cách của nó.
3.1. Các thuộc tính trong thuật toán Dijkstra
Trong thuật toán Dijkstra, mỗi đỉnh (vertex) trong đồ thị sẽ được gắn với hai thuộc tính quan trọng:
3.1.1. Visited
- Thuộc tính này cho biết liệu đỉnh đó đã được xử lý hay chưa.
- Ta sử dụng nó để tránh việc quay lại thăm một đỉnh đã hoàn tất, bởi khi một đỉnh được đánh dấu “đã thăm”, nghĩa là ta đã tìm ra đường đi ngắn nhất đến nó rồi — không cần kiểm tra lại nữa.
3.1.2. “Độ dài đường đi” (Path)
- Thuộc tính này lưu khoảng cách ngắn nhất hiện tại từ điểm xuất phát đến đỉnh đó.Ban đầu, tất cả các đỉnh đều có giá trị này là vô cùng lớn (∞), ngoại trừ đỉnh nguồn – được gán bằng 0 vì ta bắt đầu từ chính nó.
- Giá trị này sẽ liên tục được cập nhật (relax) mỗi khi ta tìm thấy một con đường ngắn hơn đi qua các đỉnh kề.
3.2. Quy trình cập nhật (Relaxation)
Sau khi chọn đỉnh nguồn và đánh dấu nó là “đã thăm”, ta sẽ duyệt qua tất cả các đỉnh kề của nó và thử cập nhật lại đường đi ngắn nhất.
Cụ thể, giả sử:
- p[v] là khoảng cách hiện tại đến đỉnh v
- p[n] là khoảng cách đến đỉnh n (đỉnh ta vừa xử lý)
- w là trọng số của cạnh nối giữa n và v
Khi đó, ta cập nhật:
p[v] = min(p[v], p[n] + w)
Nếu tổng đường đi p[n] + w nhỏ hơn giá trị cũ p[v], nghĩa là ta vừa tìm được một con đường tốt hơn để đến v.Đây chính là cốt lõi của thuật toán Dijkstra – liên tục thư giãn (relax) các cạnh để dần dần rút ngắn mọi khoảng cách trong đồ thị.
3.3. Thuật toán
Step 1: Đánh dấu đỉnh nguồn với khoảng cách hiện tại bằng 0, các đỉnh còn lại bằng vô cùng (∞).
Step 2: Chọn đỉnh chưa được thăm có khoảng cách hiện tại nhỏ nhất, gọi là C.
Step 3: Với mỗi đỉnh N kề với C, cộng khoảng cách hiện tại của C với trọng số của cạnh nối C–N. Nếu giá trị này nhỏ hơn khoảng cách hiện tại của N, thì cập nhật lại khoảng cách của N bằng giá trị mới.
Step 4: Đánh dấu C là đã thăm.
Step 5: Quay lại step2 nếu vẫn còn đỉnh chưa được thăm.
4. Ứng dụng trong tìm đường đi ngắn nhất trên map
Trong thực tế có thể áp dụng dijkstra tìm đường đi ngắn nhất trên google map hay cho các tính năng như tìm đường đi ngắn nhất trên các app giao hàng như shopee…
Cho đơn giản, ở đây xét 1 ví dụ trực quan tìm đường đi ngắn nhất từ điểm A đến F, với A là vị trí cửa hàng hiện tại, F là điểm cần giao hàng tới, và các điểm còn lại là các nút giao thông (ngã ba, ngã tư, điểm trung gian…). Khoảng cách giữa các nút giao thông là những con đường.
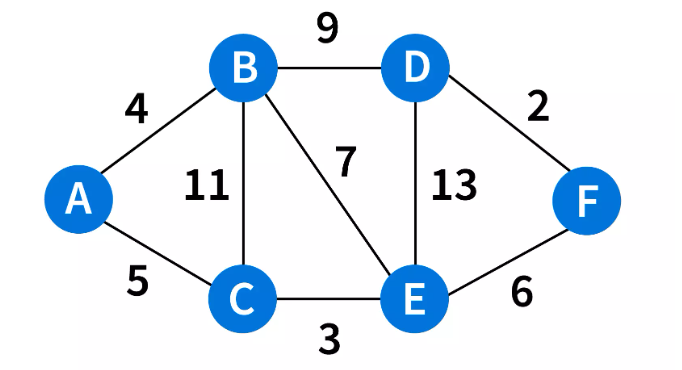
Step 1:
unvisited_node[A, B, C, D, E, F]
Step 2:
A->B = 4 A->C = 5
unvisited_node[ B, C, D, E, F]
Step 3:
B->C= 11 B->E= 7 B->D= 9
=> (A->B-> C = 14) > (A->C) = 5 -> not update C
A->B->E = 11
A->B->D = 13
unvisited_node[C, D, E, F]
Step 4:
C->E: 3 (B is visited, so C-> B not check)
=> (A->C-> E =8) < (A->B->E) = 11 -> update E = 8
unvisited_node[D, E, F]
Step 5:
D->E = 13 D->F = 2
=> A->B->D->F = 15
(A->B->D->E = 26) > (A->C->E = 8) => not update E
unvisited_node[E, F]
Step 6:
E->F = 6 (các node khác đều visited rồi nên không check lại)
=> (A->C->E->F = 14) < (A->B->D->F = 15) => update F
unvisited_node[ F]
⇒ Shortest distance from A->F = 14

Code Java
import java.util.*;
public class Main {
static final int V = 6;
static final int INF = Integer.MAX_VALUE;
// Tìm đỉnh có khoảng cách nhỏ nhất trong số các đỉnh chưa được xử lý
static int minDist(int[] dist, boolean[] sptSet) {
int min = INF, minIndex = -1;
for (int v = 0; v < V; v++) {
if (!sptSet[v] && dist[v] <= min) {
min = dist[v];
minIndex = v;
}
}
return minIndex;
}
// In kết quả
static void printSolution(int[] distance) {
System.out.println("Vertex\tDistance from Source");
for (int i = 0; i < V; i++)
System.out.println((char) (i + 65) + "\t\t" + distance[i]);
}
// Dijkstra
static void dijkstra(int[][] graph, int src) {
int[] distance = new int[V];
boolean[] sptSet = new boolean[V];
Arrays.fill(distance, INF);
Arrays.fill(sptSet, false);
distance[src] = 0;
for (int count = 0; count < V - 1; count++) {
int u = minDist(distance, sptSet);
if (u == -1) break; // phòng trường hợp không còn đỉnh hợp lệ
sptSet[u] = true;
for (int v = 0; v < V; v++) {
if (!sptSet[v] && graph[u][v] != 0 && distance[u] != INF
&& distance[u] + graph[u][v] < distance[v]) {
distance[v] = distance[u] + graph[u][v];
}
}
}
printSolution(distance);
}
public static void main(String[] args) {
// Ma trận kề biểu diễn đồ thị
// graph[i][j] = khoảng cách giữa nút giao thông i và j (0 nếu không có đường)
int[][] graph = {
{0, 4, 5, 0, 0, 0},
{4, 0, 11, 9, 7, 0},
{5, 11, 0, 0, 3, 0},
{0, 9, 0, 0, 13, 2},
{0, 7, 3, 13, 0, 6},
{0, 0, 0, 2, 6, 0}
};
int source = 0;
dijkstra(graph, source);
}
5. Độ phức tạp thuật toán
5.1. Độ phức tạp của thuật toán Dijkstra khi sử dụng ma trận kề để biểu diễn đồ thị
5.1.1. Time complexity
Giả sử đồ thị có V đỉnh.Độ phức tạp thời gian của thuật toán Dijkstra là O(V²).Giải thích như sau:
- Trước hết, ta cần tìm đỉnh chưa được thăm có độ dài đường đi nhỏ nhất.Việc này tốn O(V) thời gian vì phải duyệt qua tất cả các đỉnh.
- Với mỗi đỉnh vừa chọn, ta cần thực hiện phép “thư giãn” (relaxation) cho tất cả các đỉnh kề — tức là cập nhật lại giá trị đường đi của chúng nếu tìm được đường ngắn hơn. Mỗi lần thư giãn một đỉnh kề chỉ tốn O(1) (thời gian hằng số).
- Mỗi đỉnh có thể kề tối đa với V−1 đỉnh khác, nên việc thư giãn toàn bộ hàng xóm của một đỉnh tốn O(V).
Từ đó ta có:
- Thời gian để duyệt tất cả các đỉnh: O(V)
- Thời gian để xử lý (thư giãn) mỗi đỉnh: O(V) ⇒ Tổng thời gian: O(V × V) = O(V²)
5.1.2. Độ phức tạp bộ nhớ
Vì dùng ma trận kề kích thước V×V để lưu đồ thị, nên bộ nhớ cần là O(V²). Ngoài ra, thuật toán còn cần thêm một vài mảng kích thước V (ví dụ như distance[], visited[]), nhưng tổng thể độ phức tạp bộ nhớ vẫn là O(V²).
5.2. Khi dùng danh sách kề + hàng đợi ưu tiên (Min-Heap)
Nếu thay vì ma trận kề, ta dùng danh sách kề kết hợp Min-Heap để lưu các đỉnh chưa thăm, ta có thể giảm độ phức tạp xuống còn O((V + E) log V), với:
- E là số cạnh,
- V là số đỉnh.
Trong cách này:
- Việc duyệt qua các đỉnh có độ phức tạp O(V + E),
- Việc cập nhật (thư giãn) qua Min-Heap tốn O(log V) cho mỗi thao tác.⇒ Tổng thời gian: O((V + E) log V)
Độ phức tạp bộ nhớ trong trường hợp này cũng được cải thiện còn O(V), vì danh sách kề và Min-Heap đều chiếm không gian tỉ lệ với số đỉnh.
6. Kết luận
Qua bài viết này có thể thấy được sức mạnh của Dijkstra. Đây là một trong những thuật toán cơ bản và quan trọng nhất trong lĩnh vực lý thuyết đồ thị. Nó giúp tìm đường đi ngắn nhất từ một điểm xuất phát đến các điểm khác trong đồ thị có trọng số không âm. Với độ phức tạp O((V + E)logV) khi dùng hàng đợi ưu tiên, Dijkstra vừa hiệu quả vừa dễ triển khai. Nhờ đó, thuật toán này được ứng dụng rộng rãi trong GPS, định tuyến mạng và nhiều hệ thống tối ưu đường đi khác.
Thank you for your attention!