By Bùi Đức Toàn
“Muốn tìm trân châu nơi đáy biển, ắt phải lặn sâu. Muốn nhìn toàn cảnh rừng xanh, phải leo lên đỉnh núi.” - Cổ nhân.
Từ thuở khai hoang, con người khi thì đào sâu xuống lòng đất để tìm vàng, khi thì lại lần theo dòng sông để biết nó chảy về đâu. Trong thế giới khoa học máy tính, tinh thần khai hoang đó được tái hiện qua hai chiến lược kinh điển trong việc duyệt đồ thị là:
- Tìm kiếm theo chiều sâu (Depth-First Search – DFS).
- Tìm kiếm theo chiều rộng (Breadth-First Search – BFS).
Mọi người thường rất thân quen với việc duyệt mảng một cách tuyến tính, nhưng đôi khi dữ liệu không được lưu trữ như vậy. Việc lần theo dòng chảy của dữ liệu để tìm ra một con đường có thể tìm đến dữ liệu mà ta có chính là mục đích của DFS và BFS.
Giống như người xưa chọn đường mà đi, lúc thì tiến sâu vào từng ngách, từng lối để khám phá tận cùng, khi thì trải rộng tầm mắt, đi khắp nơi để nắm bắt toàn cục. DFS và BFS mỗi thuật toán đều mang trong mình một triết lý tìm kiếm riêng biệt.
ĐỒ THỊ - GRAPH
Trước khi đặt chân lên hành trình khám phá với chiến lược DFS và BFS thì ta cần biết vùng đất ta sẽ đi, vùng đất này chính là đồ thị (graph).
Đồ thị có hai thành phần chính để tạo nên nó, chính là:
- Đỉnh (vertices) - là các thực thể, như thành phố, ngôi làng...
- Cạnh (edges) - đại diện cho mối liên hệ giữa các đỉnh, như con đường dẫn đến các ngôi làng, thành phố.
TÌM KIẾM THEO CHIỀU SÂU - DFS
"Kẻ tìm báu vật ẩn trong động sâu, ắt phải dấn thân vào hang tối, đi đến tận cùng, rồi mới quay đầu."
Tìm kiếm theo chiều sâu (DFS) là một phương pháp tìm kiếm len lỏi qua mọi khe cùng ngõ hẻm cho đến khi không còn có thể tiến xa hơn, rồi mới quay đầu trở lại để khám phá lối khác.
Tư tưởng của DFS sẽ sử dụng cấu trúc dữ liệu Stack - ngăn xếp để thực hiện.
Cách hoạt động
- Bắt đầu từ một đỉnh (vertice) gốc đưa vào Stack.
- Lặp cho đến khi Stack rỗng:
- Lấy đỉnh trên cùng của Stack.
- Đánh dấu đỉnh vừa được lấy ra thành đã được đi đến.
- Đưa tất cả các đỉnh kề với đỉnh hiện tại vào Stack.
- Đưa đỉnh hiện tại vào mảng kết quả.
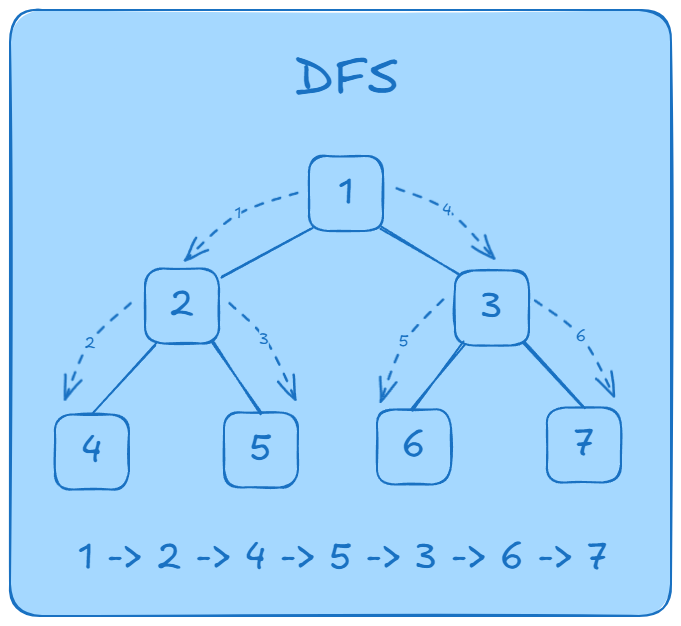
Cơ chế duyệt đồ thị
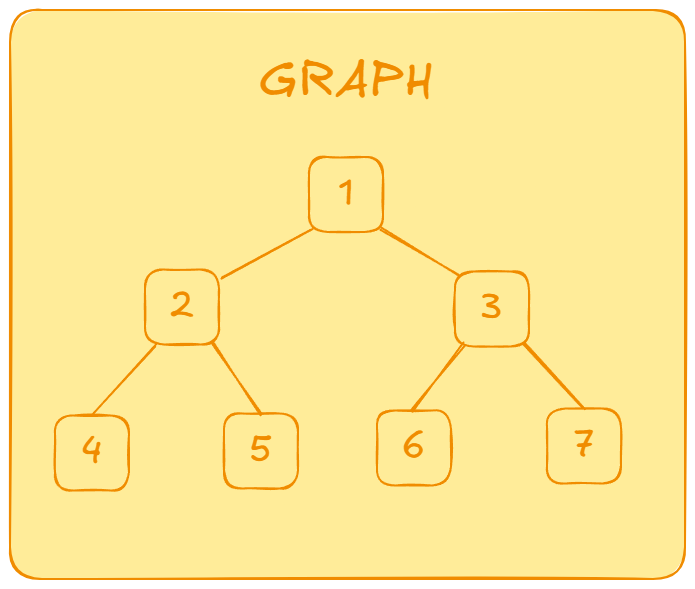
- Bắt đầu từ
1, stack:[1] - Pop
1, đánh dấu1, push3,2vào stack:[3, 2] - Pop
2, đánh dấu2, push5,4vào stack:[3, 5, 4] - Pop
4, đánh dấu4, stack:[3, 5] - Pop
5, đánh dấu5, stack:[3] - Pop
3, đánh dấu3, push7,6vào stack:[7, 6] - Pop
6, đánh dấu6, stack:[7] - Pop
7, đánh dấu7, stack:[]
Kết quả duyệt: 1 2 4 5 3 6 7 (có thể khác thứ tự nếu thứ tự các đỉnh đưa vào stack khác nhau).
TÌM KIẾM THEO CHIỀU RỘNG - BFS
"Muốn nhìn toàn cánh đồng, hãy đứng trên gò cao. Muốn hiểu cả ngôi làng, hãy đi qua từng nhà."
Khác với DFS - kẻ lữ hành thích lặng lẽ dấn bước với mọi khe cùng ngõ hẻm, BFS lại giống với một người đi tuần, chậm rãi nhưng toàn diện.Hắn là kẻ đi từng vòng, từng lớp, bắt đầu từ gốc rồi lan dần ra xa, như gợn sóng loang trên mặt hồ.
BFS là chiến lược duyệt đồ thị theo từng "lớp khoảng cách". Bắt đầu từ đỉnh gốc, nó lần lượt thăm tất cả các đỉnh kề (láng giềng gần nhất), sau đó mới đến các đỉnh xa hơn, rồi xa hơn nữa...
Tư tưởng của BFS sẽ sử dụng cấu trúc dữ liệu Queue - hàng đợi để thực hiện.
Cách hoạt động
- Bắt đầu từ một đỉnh gốc đưa vào Queue.
- Lặp cho đến khi Queue rỗng:
- Lấy đỉnh đầu tiên của Queue.
- Đánh dấu đỉnh vừa được lấy ra thành đã được đi đến.
- Đưa tất cả các đỉnh kề với đỉnh hiện tại chưa được đánh dấu vào Queue.
- Đưa đỉnh hiện tại vào mảng kết quả.
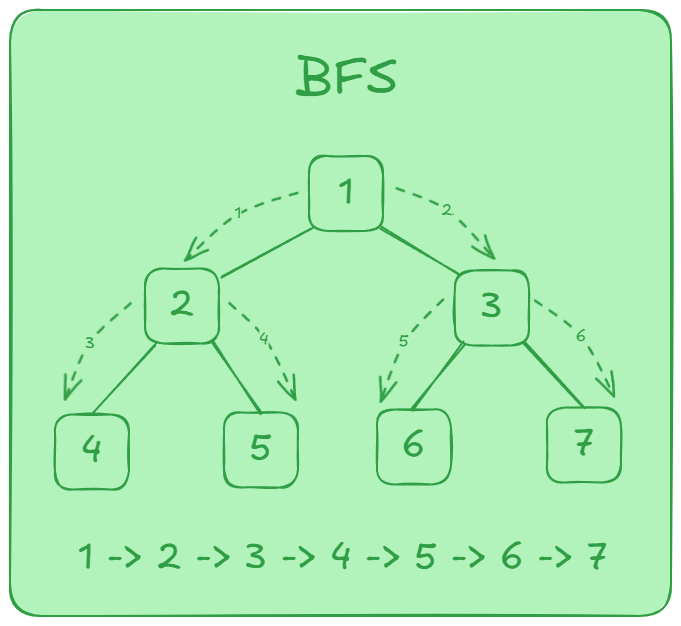
Cơ chế duyệt đồ thị
- Bắt đầu từ
1, queue:[1] - Dequeue
1, đánh dấu1, push2,3vào queue:[2, 3] - Dequeue
2, đánh dấu2, push4,5vào queue:[3, 4, 5] - Dequeue
3, đánh dấu3, push6,7vào queue:[4, 5, 6, 7] - Dequeue
4, đánh dấu4, queue:[5, 6, 7] - Dequeue
5, đánh dấu5, queue:[6, 7] - Dequeue
6, đánh dấu6, queue:[7] - Dequeue
7, đánh dấu7, queue:[]
Kết quả duyệt: 1 2 3 4 5 6 7 (có thể khác thứ tự nếu thứ tự các đỉnh đưa vào queue khác nhau).
ỨNG DỤNG TRONG TRÒ CHƠI ĐẤU TRƯỜNG CHÂN LÝ - TFT
Đồ thị không chỉ biểu thị dưới dạng cây (Tree)
"Đừng nghĩ chỉ khi bản đồ hiện rõ đỉnh và cạnh thì mới là đồ thị. Đôi khi, một bảng số cũng ẩn chứa mê cung."
Nhiều người thường nhầm lẫn rằng, chỉ khi ở dạng cây (Tree) mới là một đồ thị, nhưng không phải như thế tất cả các cấu trúc dữ liệu có đường đi, liên kết thì có thể gọi là một đồ thị. Ví dụ như array, các phần tử trong array đều liên kết với phần tử đằng sau và đằng trước nó, từ 2 có thể đi về 1 mà cũng có thể đi lên 3.
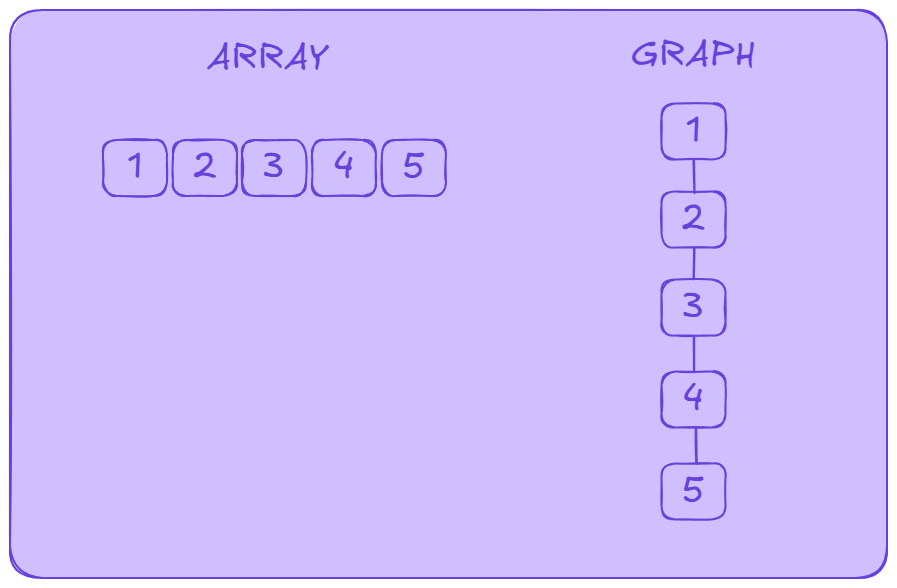
Vậy câu hỏi đặt ra là, tại sao chúng ta cần sử dụng DFS trên array và ma trận?
Tương tự với array, ma trận cũng là một đồ thị, vì vậy việc sử dụng DFS hay BFS ở đây hoàn toàn có thể, để ngắn gọn, ở đây mình dùng DFS.

Mục đích chính khi ta sử dụng DFS trên một ma trận chính là để xác định khoảng cách từ một phần tử đến một phần tử khác. Mình có một ví dụ lấy cảm hứng từ trò chơi Đấu trường Chân Lý (TFT), khi Seraphine (đứng tại ô 3) có tầm tấn công là 3, muốn kiểm tra xem khoảng cách từ cô đến Sylas (đứng tại ô 25) có nằm trong tầm tấn công không.
Các bước duyệt ma trận
B1. Bắt đầu từ 3 và khoảng cách từ 3 tới 3 là 0, stack:
[{position: 3, length: 0}]
B2. Pop {position: 3, length: 0}, đánh dấu 3, push 2, 10, 11, 4 khoảng cách so với 3 là 0 + 1 vào stack:
[{position: 2, length: 1}, {position: 10, length: 1},
{position: 11, length: 1}, {position: 4, length: 1}]
B3. Pop {position: 4, length: 1}, đánh dấu 4, push 12, 5 khoảng cách so với 3 là 1 + 1 vào stack:
[{position: 2, length: 1}, {position: 10, length: 1},
{position: 11, length: 1}, {position: 12, length: 2},
{position: 5, length: 2}]
B4. Pop {position: 5, length: 2}, đánh dấu 5, push 13, 6 khoảng cách so với 3 là 2 + 1 vào stack:
[{position: 2, length: 1}, {position: 10, length: 1},
{position: 11, length: 1}, {position: 12, length: 2},
{position: 13, length: 3}, {position: 6, length: 3}]
B5. Pop {position: 6, length: 3}, đánh dấu 6, push 14, 7 khoảng cách so với 3 là 3 + 1 vào stack:
[{position: 2, length: 1}, {position: 10, length: 1},
{position: 11, length: 1}, {position: 12, length: 2},
{position: 13, length: 3}, {position: 14, length: 4},
{position: 7, length: 4}]
B6. Pop {position: 7, length: 4}, đánh dấu 7, stack:
[{position: 2, length: 1}, {position: 10, length: 1},
{position: 11, length: 1}, {position: 12, length: 2},
{position: 13, length: 3}, {position: 14, length: 4}]
...
Khi duyệt qua hết tất cả ma trận, toàn bộ các đỉnh sẽ được đánh dấu, nhưng stack vẫn chưa rỗng, ta chỉ cần lấy khoảng cách nhỏ nhất giữa khoảng cách so với 3 của đỉnh mới và khoảng cách so với 3 của đỉnh cũ tức là lúc này, từ đỉnh 3 ban đầu có khoảng cách ngắn hơn nếu đi từ đỉnh mới.
Giả sử khi bạn ở Hà Nội, bạn muốn đi đến Hà Giang. Bạn có thể chọn cách đi vào TP. Hồ Chí Minh, xong rồi lại trở lại Hà Giang. Một cách khác là đi thẳng từ Hà Nội tới Hà Giang. Đường đi giữa hai cách sẽ khác nhau hoàn toàn, dễ thấy, ta sẽ chỉ lấy kết quả tối ưu nhất tức là từ Hà Nội tới Hà Giang để tiết kiệm chi phí.
Và sau khi duyệt xong chúng ta sẽ có kết quả như bên dưới.

Vậy lúc này với việc duyệt từ vị trí của Seraphine (ô số 3) ta chỉ cần kiểm tra ma trận khoảng cách của Seraphine tại vị trí của Sylas (ô số 25) đứng với kết quả là 3. Điều này đã trả lời được bài toán rằng Sylas đang trong tầm tấn công 3 của Seraphine và có thể gọi đến hàm tấn công để Seraphine tấn công Sylas.
KẾT LUẬN
DFS, BFS không chỉ là một thuật toán mang tính học thuật, nó là một trong nhiều cách để mọi người thấy các thế giới số kết nối. Mỗi cái mang một triết lý tìm kiếm riêng:
- Khi cần khám phá đến tận cùng, hãy nghĩ như DFS.
- Khi cần bao quát và công bằng, hãy hành xử như BFS.
Và cuối cùng, mọi cấu trúc dữ liệu đều có thể có hình bóng của đồ thị, điều quan trọng không phải nó "trông như đồ thị" mà là ta nhìn thấy đồ thị trong nó.
✏️ System Design VN: https://fb.com/groups/systemdesign.vn
📚 Đọc thêm tài liệu khác: https://roninhub.com/tai-lieu
🎬 Youtube: https://youtube.com/@ronin-engineer